二维数据SVM模拟过程

SVM 算法的基本原理。

SVM 问题描述

对于线性可分数据，二维数据决策面方程即为一元一次方程，如下：

$$y=ax+b \tag1$$

其用向量表示可以表示为：

$$\left[\begin{matrix} a & -1 \end{matrix}\right] \left[\begin{matrix} x_1 \\ x_2 \end{matrix}\right] + b = 0 \tag2 \\ \omega^Tx+\varphi = 0$$

点到直线距离方程为：

$$d=\frac{|\omega^Tx+\varphi|}{||\omega||} \tag3$$

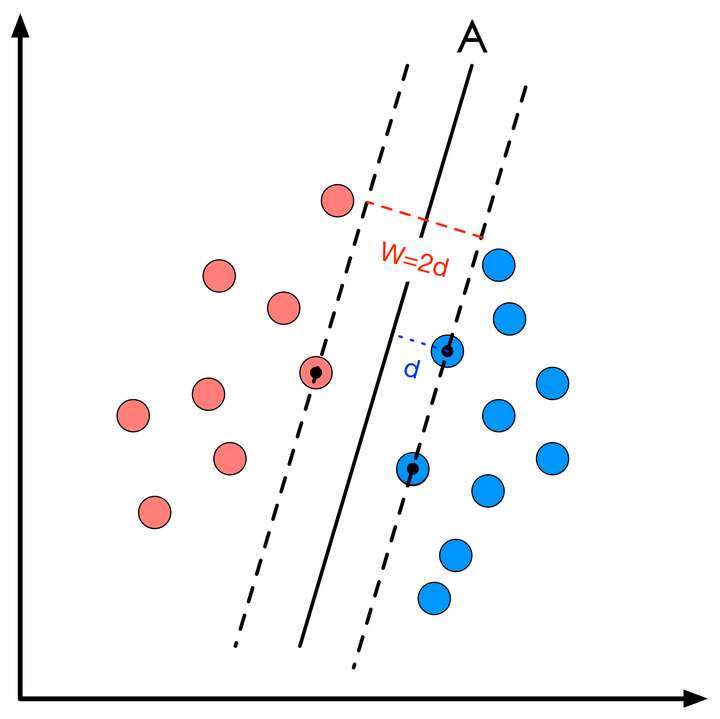
即在所有的点 $x$ 中，使得 $d$ 最大的直线即为决策面。

对每一个样本加上一个标签 $y_i$：

$$y_i = \begin{cases} +1 \ for\ y_i=1 \\ -1 \ for\ y_i=-1 \end{cases} \tag4$$

如果决策面能够完全正确的对样本进行分类，则满足：

$$\begin{cases} \omega^Tx_i+\gamma > 0 \ for\ y_i=1 \\ \omega^Tx_i+\gamma < 0 \ for\ y_i=-1 \end{cases} \tag5$$

如果决策面正好在间隔区间的中轴线上，且支持向量到决策面的距离为 $d$，那么有：

$$\begin{cases} \omega^T_dx_i+\gamma_d \ge 1 \quad for\ y_i=1 \\ \omega^T_dx_i+\gamma_d \le -1\quad for\ y_i=-1 \end{cases} \tag6 \\ 其中，\omega_d=\frac{\omega}{||\omega||d},\gamma_d=\frac{\gamma}{||\omega||d}$$

此时，令$\omega=\omega_d,\gamma=\gamma_d$，则 SVM 的优化问题的约束条件为：

$$\begin{equation} \begin{cases} \omega^Tx_i+\gamma \ge 1 \quad for\ y_i=1 \\ \omega^Tx_i+\gamma \le -1\quad for\ y_i=-1 \end{cases} \end{equation} \tag7$$

线性 SVM 优化问题基本描述

决策面的方程如 (2) 所示，所有样本点到决策面的距离为：

$$d=\frac{|\omega_Tx_i+\gamma|}{||\omega||}\ge\frac{1}{||\omega||} \tag8$$

当 $x_i$ 为支持向量时，等号成立。

式 (8) 的含义为，支持向量样本点到决策面的距离为 $\frac{1}{||\omega||}$ , 需要找到一组参数 $\omega ,\gamma$ 使得 $d$ 最小。对式 (7) 可统一表达如下：

$$y_i(\omega^Tx_i+\gamma)\ge1\quad \forall x_i \tag9$$

至此，SVM 线性最优化问题的数学描述为：

$$\begin{align*} & min_{\omega,\gamma}\frac{1}{2}||\omega||^2 \tag{10}\\ & s.t.\quad y_i(\omega^Tx_i+\gamma)\ge1,\quad i=1,2,\dots,m \end{align*}$$

---

学习自 零基础学SVM